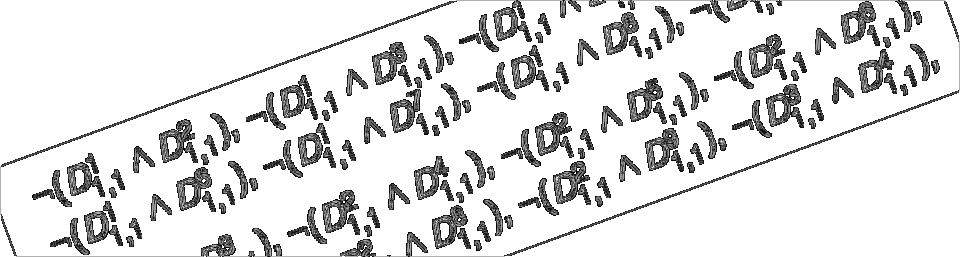@inproceedings{KochSchremppKirsten2019,
author = {Alexander Koch and
Michael Schrempp and
Michael Kirsten},
editor = {Steven D. Galbraith and
Shiho Moriai},
title = {Card-Based Cryptography Meets Formal Verification},
booktitle = {25th International Conference on the Theory and
Application of Cryptology and Information Security
({ASIACRYPT} 2019)},
abstract = {Card-based cryptography provides simple and practicable protocols for performing secure
multi-party computation (MPC) with just a deck of cards. For the sake of simplicity, this
is often done using cards with only two symbols, e.g., ♣ and ♡. Within this paper, we
target the setting where all cards carry distinct symbols, catering for use-cases with
commonly available standard decks and a weaker indistinguishability assumption. As of yet,
the literature provides for only three protocols and no proofs for non-trivial lower
bounds on the number of cards. As such complex proofs (handling very large combinatorial
state spaces) tend to be involved and error-prone, we propose using formal verification
for finding protocols and proving lower bounds. In this paper, we employ the technique of
software bounded model checking (SBMC), which reduces the problem to a bounded state
space, which is automatically searched exhaustively using a SAT solver as a backend.
\newline
Our contribution is twofold: (a) We identify two protocols for converting between
different bit encodings with overlapping bases, and then show them to be card-minimal.
This completes the picture of tight lower bounds on the number of cards with respect to
runtime behavior and shuffle properties of conversion protocols. For computing AND, we
show that there is no protocol with finite runtime using four cards with distinguishable
symbols and fixed output encoding, and give a four-card protocol with an expected finite
runtime using only random cuts. (b) We provide a general translation of proofs for lower
bounds to a bounded model checking framework for automatically finding card- and
length-minimal protocols and to give additional confidence in lower bounds. We apply this
to validate our method and, as an example, confirm our new AND protocol to have a
shortest run for protocols using this number of cards.},
venue = {Kobe, Japan},
eventdate = {2019-09-08/2019-09-12},
month = nov,
series = {Lecture Notes in Computer Science},
volume = {11921},
part = {I},
pages = {488--517},
publisher = {Springer},
year = {2019},
doi = {10.1007/978-3-030-34578-5_18}
}
Card-Based Cryptography Meets Formal Verification
| Author(s): | Alexander Koch, Michael Schrempp, and Michael Kirsten |
|---|---|
| In: | 25th International Conference on the Theory and Application of Cryptology and Information Security (ASIACRYPT 2019) |
| Publisher: | Springer |
| Series: | Lecture Notes in Computer Science |
| Volume: | 11921 |
| Part: | I |
| Year: | 2019 |
| Pages: | 488-517 |
| PDF: | IACR ePrint |
| DOI: | 10.1007/978-3-030-34578-5_18 |
Abstract
Card-based cryptography provides simple and practicable protocols for performing secure
multi-party computation (MPC) with just a deck of cards. For the sake of simplicity, this
is often done using cards with only two symbols, e.g., ♣ and ♡. Within this paper, we
target the setting where all cards carry distinct symbols, catering for use-cases with
commonly available standard decks and a weaker indistinguishability assumption. As of yet,
the literature provides for only three protocols and no proofs for non-trivial lower
bounds on the number of cards. As such complex proofs (handling very large combinatorial
state spaces) tend to be involved and error-prone, we propose using formal verification
for finding protocols and proving lower bounds. In this paper, we employ the technique of
software bounded model checking (SBMC), which reduces the problem to a bounded state
space, which is automatically searched exhaustively using a SAT solver as a backend.
Our contribution is twofold: (a) We identify two protocols for converting between
different bit encodings with overlapping bases, and then show them to be card-minimal.
This completes the picture of tight lower bounds on the number of cards with respect to
runtime behavior and shuffle properties of conversion protocols. For computing AND, we
show that there is no protocol with finite runtime using four cards with distinguishable
symbols and fixed output encoding, and give a four-card protocol with an expected finite
runtime using only random cuts. (b) We provide a general translation of proofs for lower
bounds to a bounded model checking framework for automatically finding card- and
length-minimal protocols and to give additional confidence in lower bounds. We apply this
to validate our method and, as an example, confirm our new AND protocol to have a
shortest run for protocols using this number of cards.