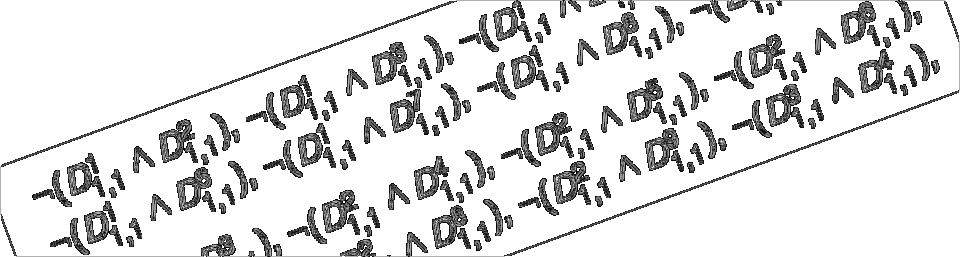@inproceedings{kernSinz2024,
author = {Philipp Kern and Carsten Sinz},
editor = {Roberto Giacobazzi and Alessandra Gorla},
title = {Abstract Interpretation of ReLU Neural Networks with Optimizable Polynomial Relaxations},
booktitle = {31st Symposium on Static Analysis ({SAS} 2024), Pasadena, USA, October 20-22, 2024},
year = {2024},
month = oct,
publisher = {Springer Nature Switzerland},
address = {Cham},
pages = {173--193},
abstract = {Neural networks have been shown to be highly successful in a wide range of
applications. However, due to their black box behavior, their applicability can be
restricted in safety-critical environments and additional verification techniques
are required. Many state-of-the-art verification approaches use abstract interpretation
based on linear overapproximation of the activation functions. Linearly approximating non-
linear activation functions clearly incurs a loss of precision. One way to overcome this
limitation is the utilization of polynomial approximations. A second way shown to improve
the obtained bounds is to optimize the slope of the linear relaxations. Combining these
insights, we propose a method to enable similar parameter optimization for polynomial
relaxations. Given arbitrary values for a polynomial's monomial coefficients, we can
obtain valid polynomial overapproximations by appropriate upward or downward shifts.
Since any value of monomial coefficients can be used to obtain valid overapproximations
in that way, we use gradient-based methods to optimize the choice of the monomial coefficients.
Our evaluation on verifying robustness against adversarial patches on the MNIST and CIFAR10
benchmarks shows that we can verify more instances and achieve tighter bounds than
state of the art bound propagation methods.},
isbn = {978-3-031-74776-2},
doi = {10.1007/978-3-031-74776-2_7}
}
Abstract Interpretation of ReLU Neural Networks with Optimizable Polynomial Relaxations
| Author(s): | Philipp Kern and Carsten Sinz |
|---|---|
| In: | 31st Symposium on Static Analysis (SAS 2024), Pasadena, USA, October 20-22, 2024 |
| Publisher: | Springer Nature Switzerland |
| Year: | 2024 |
| Pages: | 173-193 |
| DOI: | 10.1007/978-3-031-74776-2_7 |
Abstract
Neural networks have been shown to be highly successful in a wide range of applications. However, due to their black box behavior, their applicability can be restricted in safety-critical environments and additional verification techniques are required. Many state-of-the-art verification approaches use abstract interpretation based on linear overapproximation of the activation functions. Linearly approximating non- linear activation functions clearly incurs a loss of precision. One way to overcome this limitation is the utilization of polynomial approximations. A second way shown to improve the obtained bounds is to optimize the slope of the linear relaxations. Combining these insights, we propose a method to enable similar parameter optimization for polynomial relaxations. Given arbitrary values for a polynomial's monomial coefficients, we can obtain valid polynomial overapproximations by appropriate upward or downward shifts. Since any value of monomial coefficients can be used to obtain valid overapproximations in that way, we use gradient-based methods to optimize the choice of the monomial coefficients. Our evaluation on verifying robustness against adversarial patches on the MNIST and CIFAR10 benchmarks shows that we can verify more instances and achieve tighter bounds than state of the art bound propagation methods.