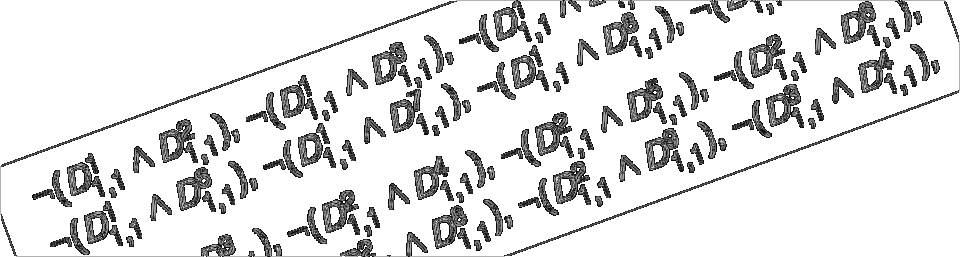@InProceedings{MU20,
author = {Laura Merker and
Torsten Ueckerdt},
editor = {David Auber and
Pavel Valtr},
title = {The Local Queue Number of Graphs with
Bounded Treewidth},
booktitle = {28th International Symposium on Graph Drawing and
Network Visualization ({GD} 2020), Revised
Selected Papers},
venue = {Vancouver, {BC}, Canada},
eventdate = {2020-09-16/2020-09-18},
series = {Lecture Notes in Computer Science},
volume = {12590},
pages = {26--39},
publisher = {Springer},
year = {2020},
abstract = {A queue layout of a graph G consists of a vertex ordering
of G and a partition of the edges into so-called queues
such that no two edges in the same queue nest, i.e., have
their endpoints ordered in an ABBA-pattern. Continuing
the research on local ordered covering numbers, we
introduce the local queue number of a graph G as the
minimum ℓ such that G admits a queue layout with each
vertex having incident edges in no more than ℓ queues.
Similarly to the local page number [Merker and Ueckerdt,
GD'19], the local queue number is closely related to the
graph's density and can be arbitrarily far from the
classical queue number.},
doi = {10.1007/978-3-030-68766-3_3},
url = {https://arxiv.org/abs/2008.05392}
}
Zurück zur Hauptseite von "Praxis der Forschung"
Praxis der Forschung
The Local Queue Number of Graphs with Bounded Treewidth
| Autor(en): | Laura Merker und Torsten Ueckerdt |
|---|---|
| In: | 28th International Symposium on Graph Drawing and Network Visualization (GD 2020), Revised Selected Papers |
| Verleger: | Springer |
| Reihe: | Lecture Notes in Computer Science |
| Band: | 12590 |
| Jahr: | 2020 |
| Seiten: | 26-39 |
| URL: | https://arxiv.org/abs/2008.05392 |
| DOI: | 10.1007/978-3-030-68766-3_3 |
Abstract
A queue layout of a graph G consists of a vertex ordering of G and a partition of the edges into so-called queues such that no two edges in the same queue nest, i.e., have their endpoints ordered in an ABBA-pattern. Continuing the research on local ordered covering numbers, we introduce the local queue number of a graph G as the minimum ℓ such that G admits a queue layout with each vertex having incident edges in no more than ℓ queues. Similarly to the local page number [Merker and Ueckerdt, GD'19], the local queue number is closely related to the graph's density and can be arbitrarily far from the classical queue number.